Teorema lui Pick, matematica care imi plac

Să considerăm un poligon nedegenerat simplu întreg (adică conectat - oricare două puncte pot fi conectate printr-o curbă continuă, în întregime conținute în acesta și toate nodurile sale au coordonatele întreg, limita ei - conectat poligon fără auto-intersecții și are nenulă suprafață) .

Pentru a calcula aria poligonului, puteți utiliza următoarea teoremă:

Teorema lui Pick. Să presupunem că - numărul de puncte întregi în interiorul poligonului, - numărul de puncte întregi pe limita, - aria sa. Apoi, următoarea formulă Vârf:

Exemplu. Pentru poligon în figură (puncte galbene), (puncte albastre, nu uita topuri!), Astfel încât unitățile pătrate.

Aici puteți face pentru a construi o varietate de poligoane, iar zona în care vor fi calculate prin formula Vârful (poligoane prezente în acest articol, este construit acolo).

Alege Dovada teoremei. În primul rând, observăm că formula este adevărată pentru alegerea unității pătrat. Într-adevăr, în acest caz, avem amândoi.

Luați în considerare un dreptunghi cu laturile situată pe liniile grilei. Să lungimilor laturile sale sunt egale și. Avem în acest caz, formula alege,

Să considerăm acum un triunghi dreptunghic cu picioare situate pe axele de coordonate. Un astfel de triunghi se obține din dreptunghi cu laturile și discutate în cazul precedent, prin tăiere în diagonală. Să se află pe punctele întregi diagonale. Întrucât, în acest caz, se dovedește că

Acum, ia în considerare un triunghi arbitrar. Acesta poate fi obținut prin tăierea dreptunghiului de mai multe triunghiuri dreptunghiulare și, eventual, dreptunghi (vezi. Figurile). În ceea ce privește dreptunghi, și pentru triunghiul Pick de formula unghi drept este adevărat, vom vedea că este, de asemenea, valabil pentru un triunghi arbitrar.

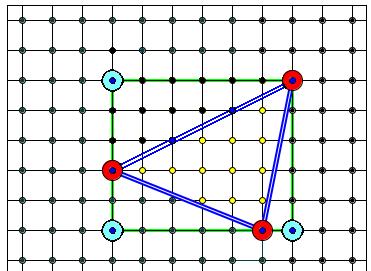
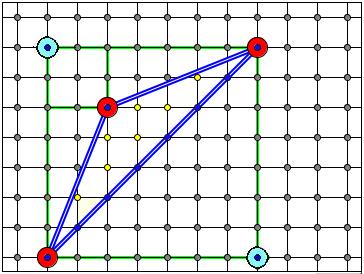
Rămâne de a lua ultimul pas: du-te la triunghiuri la poligoane. Orice poligon poate fi divizat în triunghiuri (de exemplu diagonală). Prin urmare, trebuie doar să dovedească faptul că adăugarea oricărui triunghi teorema unui poligon arbitrar pick este adevărat.

Să presupunem că un poligon, și un triunghi au o latură comună. Să presupunem că pentru formula de vârf validă dovedesc că este adevărat pentru poligon care rezultă din adăugarea. Din moment ce ambele au o latură comună, atunci toate punctele de pe această parte integrantă, dar două noduri sunt puncte interioare ale noului poligonului. Vârfurile vor fi, de asemenea, punctele de frontieră. Notăm numărul de puncte în comun se obține prin

- numărul de puncte întregi interioare ale noului poligon

- numărul de puncte de frontieră ale noului poligon.

Din aceste ecuații vom obține

Din moment ce am presupus că teorema este adevărată pentru și separat,

Astfel, Teorema lui Pick dovedit.

Din păcate, această formulă remarcabilă nu se generaliza la dimensiuni mai mari, chiar și în cazul tridimensional. Acesta a aratat Reeve. Luați în considerare Riva tetraedru, ale căror vârfuri au coordonate

(Aici -. Număr natural) Pentru orice în interiorul acestui tetraedru nici un punct întreg, și nu există puncte întregi pe limita, cu excepția și. Astfel, la diferite volume și suprafețe de zone date tetraedre număr întreg de puncte care se găsesc în interiorul lor și la limitele lor, rămâne neschimbată, și sinteza Formula vârf nu poate fi obținut.

Cu toate acestea, unele generalizări obținute prin polinoame Ehrhart.