plan înclinat
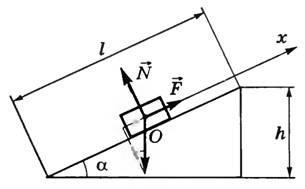
Planul înclinat este o suprafață plană dispusă la orice unghi față de orizontală. Acesta vă permite să ridice sarcina cu o forță mai mică decât în cazul în care sarcina este ridicată pe verticală în sus. Pe un plan înclinat de sarcină se ridică de-a lungul acestui plan. În același timp, el depășește o distanță mai mare decât în cazul în care se ridică pe verticală.
Și de câte ori există un câștig în putere atât de multe ori nu va fi mai la distanță, care va depăși sarcina.

Figura 1. planul înclinat
În cazul în care înălțimea la care este necesar pentru a ridica o sarcină, egală cu $ h $, și, astfel, ar fi fost cheltuit forță $ F_h $, iar lungimea planului înclinat de $ l $, și, astfel, a cheltuit forță $ f_l $, atunci $ l $ ca se refera la $ h $ la $ F_h $ apartine $ f_l $: $ l / h = F_h / f_l $. Cu toate acestea, $ F_h $ - este greutatea sarcinii ($ P $). Deci, este de obicei scris ca: $ l / h = P / F $, în cazul în care $ F $ - forță pentru a ridica o sarcină.
Forța $ F $, care trebuie aplicată sarcina de cântărire $ P $ la corp a fost în echilibru pe un plan înclinat este egal cu $ F_1 = R_h / l = Rsin $ dacă forța aplicată $ P $ paralelă plan înclinat (Figura 2, a) și $ F_2 $ = $ R_h / l = Rtg $ dacă forța F $ $ aplicată paralel cu planul înclinat bază (Figura 2b).
Rezolvarea controlului în toate subiectele. 10 ani de experiență! Preț de la 100 de ruble. Perioada de la 1 zi!

Figura 2. Deplasarea încărcăturii de-a lungul planului înclinat
a) forță paralelă cu planul b) forța este paralelă cu solul
Înclinat Plane dă câștigul în putere, acesta poate fi folosit pentru a ridica sarcina la o înălțime mai ușor. Mai mic unghiul $ \ alpha $, cu atât mai mare câștig în putere. În cazul în care unghiul de $ \ $ alfa este mai mică decât unghiul de frecare, sarcina nu se va muta în mod spontan, și avem nevoie de un efort de a-l trage în jos.
Dacă luăm în considerare forța de frecare dintre sarcina și planul înclinat, apoi pentru $ F_1 $ și $ F_2 $ obținut următoarele valori: $ F_1 = Rsin ($$$$ \ pm $$$) / cos $$; $ F_2 = Rtg ($$$$ \ pm $$$)
Semnul plus se referă la mișcarea în sus, semnul minus - la reducerea sarcinii. Eficiența planului înclinat $$ 1 = sin $$ cos $$ / sin ($$ + $$), în cazul în care forța F $ $ îndreptate paralel cu planul și 2 $$ = tg $$ / tg ($$ + $$), în cazul în care forța F $ $ este paralel cu baza planului înclinat.
Rezolvarea controlului în toate subiectele. 10 ani de experiență! Preț de la 100 de ruble. Perioada de la 1 zi!
Un plan înclinat supus „regula de aur a mecanicii“. Mai mic unghiul dintre suprafața și planul înclinat (m. E. Este mult mai plat nu este în creștere abrupt în sus), cu atât mai puțin necesar să se aplice forța pentru a ridica sarcina, dar, de asemenea, distanța mai mare de a fi depășite.
În absența frecării forțează câștigul în putere $ K = P / F = 1 / păcatul $$ \ alpha = l / h $. În condiții reale, datorită forței de frecare actioneaza eficiența plan înclinat este mai mică de 1, câștigul în raport rezistență mai mică $ l / h $.
O greutate de 40 kg este ridicată de-a lungul planului înclinat la o înălțime de 10 m timp ce se aplică o forță de 200 N (figura 3). Care este lungimea rampei? Frecare neglijate.
= \ Frac = \ frac \ >> $. Prin urmare, $ l = \ frac = \ \ frac = 5,1 \ m $.
A: lungimea înclinată plane 5.1 m
Două corpuri cu mase $ M_1 $ = 10 și r $ m_2 $ = asociat 15g de fir aruncate printr-o unitate fixă instalată pe un plan înclinat (fig. 4). Plane formează un unghi cu orizont $ \ alpha $ = $ la 30<>^ \ $ Circ. Găsiți accelerația, care se va muta corpul.

Directăm axa x de-a lungul planului înclinat, iar axa OY - perpendicular pe ea, și am proiecta aceste vector de axa $ \> _ 1 \ și \> _ 2 $. După cum se poate observa din figură, rezultanta forțelor aplicate fiecăruia dintre organismele este egală cu diferența dintre proiecțiile $ \> _ 1 \ și \> _ $ 2 de pe axa x:
corpuri de accelerare $ a_1 = 2,45 \ Frac; \ \ \ \ \ \ a_2 = 1,63 \ m / s ^ 2 $: Răspuns