Perioada Pendulum și accelerare cu formula
Sistemul mecanic care constă dintr-un punct material (corp), care atârnă pe un filament inextensibil imponderabilă (masa sa este neglijabilă în raport cu greutatea corpului) într-un câmp gravitațional uniform, numit pendulul matematic (un alt nume - oscilator). Există și alte tipuri de dispozitive. In loc de o tijă imponderabilă filament poate fi utilizat. Pendulul poate dezvălui în mod clar esența multor fenomene interesante. Atunci când vibrațiile mică amplitudine ale mișcării sale se numește armonice.
Informații generale despre sistemul mecanic

Dacă pendulul este într-o poziție de echilibru (agățat pe verticală), forța de gravitație va fi echilibrată de forța de tensionare fire. pendul plat pe o fire neextensibil este un sistem cu două grade de libertate de comunicare. La schimbarea doar o componentă a schimba caracteristicile tuturor părților sale. De exemplu, dacă un fir este înlocuit cu o tijă, atunci acest sistem mecanic este de numai 1 grad de libertate. Ceea ce, atunci, proprietățile unui pendul matematic? În acest sistem simplu, sub influența unei perturbație periodice, apare haosul. În acest caz, atunci când punctul de suspensie nu este în mișcare, iar penduleaza un pendul există o nouă poziție de echilibru. În cazul în care fluctuațiile rapide în sus și în jos acest sistem mecanic devine poziție stabilă „cu susul în jos.“ Ea are, de asemenea, numele său. Se numește Kapitza pendulul.
Proprietățile pendulului
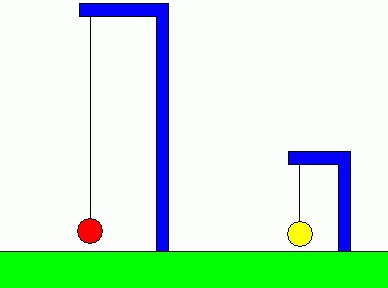
• În cazul în care, menținând în același timp aceeași lungime a pendulului, suspendat dintr-o varietate de sarcini, perioada de oscilație a obține același lucru, cu toate că greutatea lor va varia foarte mult. În consecință, perioada pendulului nu depinde de greutatea sarcinii.
• În cazul în care sistemul începe să scadă în pendulului nu este prea mare, dar unghiuri diferite, acesta va fluctua cu aceeași perioadă, dar la amplitudini diferite. În timp ce abateri de la centrul de echilibru nu este fluctuații prea mari în forma lor va fi destul de aproape armonic. Perioada de un astfel de pendul nu depinde de amplitudinea de vibrație. Această proprietate a sistemului mecanic se numește isochronism (în „Chronos“ greacă - timp „Izosov“ - egal).
Perioada unui pendul simplu
Această cifră reprezintă perioada de oscilație naturală. În ciuda formulării complexe, procesul în sine este foarte simplu. Dacă lungimea firului matematic pendul L, iar accelerația gravitațională g, această valoare este egală cu:
Perioada de mici oscilații naturale în nici un fel nu depinde de masa pendulului și amplitudinea de oscilație. În acest caz, ca un pendul matematic se mișcă cu o lungime redusă.
Oscilațiilor unui pendul matematic
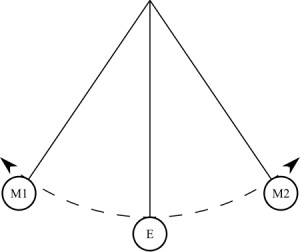
pendulului matematic pendulează, care poate fi descrisă printr-o ecuație diferențială simplă:
x + ω2 sin x = 0,
unde x (t) - funcții necunoscute (acest unghi de deviere de la poziția inferioară de echilibru la momentul t, exprimat în radiani); ω - o constantă pozitivă care este determinată de parametrii pendulului (ω = √g / L, unde g - accelerația gravitațională, și L - lungimea unui pendul simplu (suspensie).
Ecuația mici oscilații in poziție de echilibru (ecuația armonică) după cum urmează:
x + ω2 sin x = 0
mișcarea oscilatorie a pendulului
Pendulum, ceea ce face mici oscilații, se deplasează sinusoidă. A doua ecuație diferențială îndeplinește toate cerințele și parametrii unei astfel de mișcări. Pentru a determina calea pe care trebuie să setați viteza și coordonate, care au determinat ulterior constante independente:
x = A sin (θ0 + ωt),
unde θ0 - faza inițială, A - amplitudinea de oscilație, ω - frecvența ciclică determinată din ecuațiile de mișcare.
Pendulum (formula pentru amplitudini mari)
Acest sistem mecanic, efectuează oscilații lor, cu o amplitudine mare, este supusă unor legi mai complexe de trafic. acestea sunt calculate conform formulei pentru un astfel de pendul:
sin x / 2 = u * sn (ωt / u),
în cazul în care sn - sinus Jacobi, care pentru u <1 является периодической функцией, а при малых u он совпадает с простым тригонометрическим синусом. Значение u определяют следующим выражением:
u = (ε + ω2) / 2ω2,
unde ε = E / ML2 (ML2 - energia pendulului).
Determinarea perioadei de oscilație neliniare a pendulului prin următoarea formulă:
unde ω = π / 2 * ω / 2K (u), K - eliptic integral, π - 3,14.
mișcarea pendulului a separatrix
Se numește separatrix traiectorie a sistemului dinamic, în care un spațiu de fază bidimensional. Pendulum se mută pe un non-periodic. În punctul infinit de departe de timp scade din poziția superioară extremă spre o viteză zero, iar apoi se câștigă treptat. în cele din urmă a oprit, revenind la poziția inițială.
În cazul în care amplitudinea de oscilație a pendulului se apropie de numărul tt. acest lucru sugerează că mișcarea în planul de fază este aproape de separatrix. În acest caz, sub acțiunea unei mici forță motrice periodică a sistemului mecanic prezintă un comportament haotic.
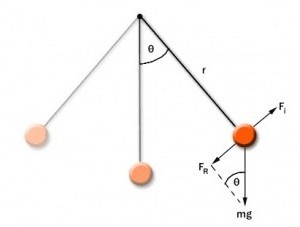
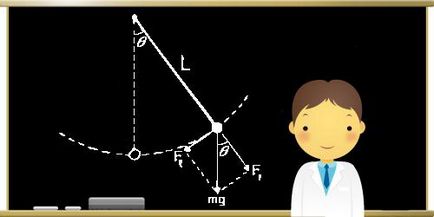
În cazul unui pendul simplu din poziția de echilibru cu un unghi cp are loc forță tangențială Fτ = -Mg păcat φ gravitația. „Minus“ semn înseamnă că componenta tangențială îndreptată în direcția opusă direcției de deviere a pendulului. Când se face referire prin deplasarea cu pendul x de-a lungul unui arc de cerc cu raza L este egală cu deplasarea unghiulară φ = x / L. A doua lege a Isaaka Nyutona, conceput pentru proiecția vectorului accelerație și puterea da valoarea dorită:
mg τ = Fτ = -Mg sin x / L
Pe baza acestui raport, este clar că pendulul este un sistem neliniar, ca o forță care tinde să revină la poziția sa de echilibru, nu este întotdeauna proporțională cu deplasarea x, un sin x / L.
Numai atunci când pendulul matematic efectuează vibrații mici, este un oscilator armonic. Cu alte cuvinte, acesta devine un sistem mecanic capabil să efectueze oscilații armonice. Această aproximare este valabilă pentru aproape unghiuri de 15-20 °. Pendulul cu amplitudini mari nu este armonios.
legea lui Newton pentru oscilații mici ale unui pendul

Dacă sistemul mecanic efectuează oscilații mici, legea lui Newton doilea va arata astfel:
mg τ = Fτ = -m * g / L * x.
Pe această bază, putem concluziona că accelerația tangențială a unui pendul simplu este proporțională cu deplasarea acestuia cu semnul „minus“. Aceasta este o condiție prin care sistemul devine un oscilator armonic. Modul factor de proporționalitate între deplasarea și accelerația este egală cu pătratul frecvenței unghiulare:
ω02 = g / l; ω0 = √ g / L.
Această formulă reflectă frecvența naturală a oscilații mici ale acestui tip de pendul. Pe această bază,
T = 2π / ω0 = 2π√ g / L.
Calculele bazate pe legea de conservare a energiei
Proprietăți oscilante mișcările pendulului poate fi descrisă cu ajutorul legii de conservare a energiei. Trebuie avut în vedere faptul că energia potențială a pendulului într-un câmp gravitațional este:
E = mgΔh = MGL (1 - cos α) = mgL2sin2 α / 2
Energia mecanică totală este egală cu cinetică și potențială maximă: Epmax = Ekmsx = E
După ce ați scris legea conservării energiei, luând derivata din partea stângă și dreaptă ale ecuației:
Deoarece derivatul constantelor este egal cu 0, atunci (Ep + Ek) „= 0. Derivatul sumei este egală cu suma derivatelor:
Ep '= (mg / L * x2 / 2)' = mg / 2L * 2x * x '= mg / L * v + Ek' = (MV2 / 2) = m / 2 (v2) „= m / 2 * 2v * v „= mv * α,
Mg / L * xv + AVM = v (mg / L * x + m α) = 0.
Bazat pe ultima formula, descoperim: α = - g / L * x.
Aplicarea practică a pendulului matematic
accelerația gravitațională variază în funcție de latitudine, deoarece densitatea crustei în jurul planetei nu identice. În cazul în care apar roci cu o densitate mai mare, acesta va fi ușor mai ridicate. Accelerarea pendulului matematic este adesea folosit pentru explorare. În aspectul său de ajutor pentru diferite minerale. Pur și simplu numărarea numărului de oscilații ale unui pendul, este posibilă detectarea cărbunelui sau minereului în măruntaiele pământului. Acest lucru se datorează faptului că aceste resurse au o densitate și greutate mai mare situată sub rocile.
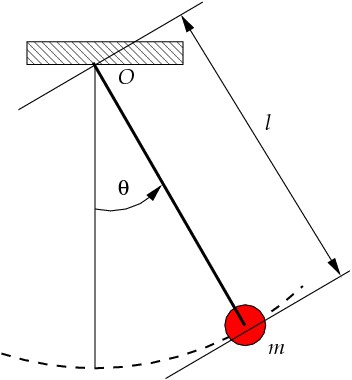
pendul matematic folosit de astfel de savanți proeminenți precum Socrate, Aristotel, Platon, Plutarh, Arhimede. Mulți dintre ei au crezut că sistemul mecanic poate influența soarta și viața. Arhimede a folosit pendulul matematic cu calculele sale. In zilele noastre, mulți ocultiști și văzătorii folosesc acest sistem mecanic pentru punerea în aplicare a profețiilor sale, sau căutarea persoanelor dispărute.
Celebrul astronom și om de știință francez, Flammarion pentru cercetarea lor, de asemenea, folosit un pendul matematic. El a susținut că, cu ajutorul lui el a fost capabil să prezică descoperirea unei noi planete, apariția meteoritului Tunguska, și alte evenimente importante. În timpul al doilea război mondial în Germania (Berlin), a lucrat ca un institut de specialitate al pendulului. În prezent, o astfel de cercetare nu este disponibil Institutul de Parapsihologie Munchen. Munca lui cu pendulul personalul acestei instituții numită „radiesteziey“.
