oscilațiile electromagnetice - studopediya

Fluctuații numita mișcare sau procese care sunt caracterizate printr-o anumită repetiție în timp. Fluctuații pot fi diferite în natura lor fizică (mecanică, electromagnetică, gravitație), dar ele sunt descrise prin aceleași ecuații cu structura.

Cel mai simplu tip de vibratii sunt vibratii armonice. în care valoarea fluctuant variază armonic, t. e. ca o funcție sinus sau cosinus.

Fluctuațiile sunt gratuite și forțată. oscilații gratuite separate în neamortizate (propriu) și cu amortizare.

oscilații neamortizate sau proprii libere - aceste fluctuații care apar datorită energiei sistemului oscilant comunicate la momentul inițial, când nu mai departe influență externă asupra sistemului.

Ecuația diferențială a propriei sale kolebaniykontura undei electrice (Fig. 4.1)

,

în care - sarcina electrică a condensatorului; - ciclică de frecvență (circulară) de oscilație liberă undamped (aici - bucla inductanță - capacitate circuit electric).

Ecuația oscilații armonice electrice:

,

în care - amplitudinea taxei condensatorului; - faza inițială.

Curentul din circuit oscilant

,

în cazul în care - amplitudinea intensitate a curentului.

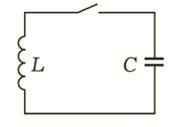
Fig. 4.1. Circuitul ideal oscilație

Perioada de oscilație - pe parcursul unei oscilație completă. În acest timp, faza de oscilație este incrementat.

Frecvența de oscilație - numărul de oscilații efectuate pe unitatea de timp,

.

Formulele aferente perioadei, frecvența și frecvența ciclică:

; ; .

Perioada de oscilații neamortizate libere în circuitul oscilatorie se determină prin formula electromagnetică Thomson

.

Amplitudinea fluctuațiilor de sarcină nete care apar în două contururi diferite și pliabilă pe o singură sarcină (oscilații pliabile într-o singură direcție și aceeași frecvență)

,

și în care - amplitudinea celor două oscilații; și - faza inițială a celor două oscilații.

Faza inițială a fluctuațiilor de sarcină care rezultă implicat în două oscilații într-o singură direcție și cu aceeași frecvență,

.

.. Ecuația bate, oscilații adică non-armonice induse de oscilații armonice de suprapunere ale căror frecvențe sunt destul de aproape:

,

în cazul în care - amplitudinea bătăii; - frecvența bătăilor.

Ecuația traiectoriei taxei. implicat în două oscilații perpendiculare reciproc ale aceeași frecvență:

.

oscilațiile gratuite cu amortizare - aceste oscilații ale căror amplitudine scade cu timpul din cauza pierderilor de energie ale sistemului vibrante. Într-un circuit rezonant electric pe energia consumată de căldură Joule și radiații electromagnetice.

Ecuația diferențială a oscilației amortizată în circuitul electric care are o rezistență electrică:

,

în care: - coeficientul de amortizare (aici - inductanța circuitului).

Ecuația oscilație amortizată în cazul slab de amortizare () (Figura 4.2.):

,

în care - amplitudinea de oscilație amortizată taxa condensator; - amplitudinea inițială a oscilațiilor; - frecvența ciclică oscilație amortizată.

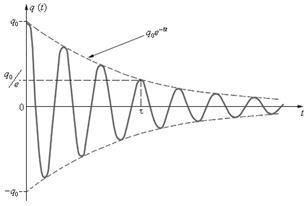
Fig. 4.2. Modificarea în timp a taxei de la oscilații amortizate mici

Timpul de relaxare - un interval de timp în care amplitudinea de oscilație se diminuează din nou:

.

Timpul de relaxare este legată de raportul dintre coeficientul de amortizare

.

Descrestere logaritmica a oscilațiilor de amortizare

,

în care: - perioada de oscilații amortizate.

Formula privind decrementul logaritmică a oscilațiilor coeficientul de amortizare și perioada de oscilații amortizate:

.

oscilații forțate - l astfel de oscilații care au loc în prezența unui impact extern variază periodic.

Ecuația diferențială de oscilație forțată în circuitul electric care are o rezistență electrică, în prezența forței electromotoare motrice variabilă sinuos, în cazul în care - valoarea amplitudinii emf, și - modificarea frecvenței ciclică a EMF: (Figura 4.3.)

,

în care: - coeficientul de amortizare; - Circuit inductanță.

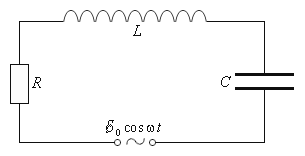
Fig. 4.3. Circuit pentru monitorizarea oscilații electrice pe plan intern

Ecuația oscilații electrice la starea de echilibru:

,

în care - diferența de fază pentru a încărca condensatorul și oscilație motrice sursa de alimentare a CEM.

Amplitudinea la starea de echilibru taxa de oscilație condensator

.

Diferența de fază și condensator de oscilație curent de încărcare emf sursă de conducere

.

Amplitudinea oscilațiilor forțate depinde de raportul dintre frecvența ciclică a oscilațiilor de conducere și de feedback. Rezonant frecvența și amplitudinea de rezonanță:

; .