Cum se calculează distanța

Distanța (notată cu d) - este lungimea unei linii drepte între două puncte. Distanța poate fi găsită între două puncte fixe, și este posibil să se găsească distanța parcursă de către corpul în mișcare. In cele mai multe cazuri, distanța poate fi calculată cu ajutorul următoarelor formule: d = s × t, unde d - distanța, s - viteza de, t - timp; d = √ ((x2 - x1) 2 + (y2 - y1) 2. unde (x1 y1) și (x2 y2) - .. coordonatele a două puncte.

pași Editare

Metoda 1 de la 2:
Calcularea distanței și viteza de timp Editare

Pentru a calcula distanța parcursă de către corpul în mișcare, trebuie să știți viteza corpului și timpul de călătorie și să le înlocuiască în formula d = s × T.

• Exemplu. Vehiculul se deplasează cu o viteză de 120 km / h timp de 30 minute. Este necesar să se calculeze distanța parcursă.

Înmulțiți viteza și timpul și veți găsi distanța.

• Să acorde o atenție la unitatea valorilor de măsurare. Dacă acestea sunt diferite, aveți nevoie pentru a converti una dintre ele, astfel încât să se potrivească unul cu altul. În exemplul nostru, viteza măsurată în kilometri pe oră, iar timpul - în câteva minute. Prin urmare, este necesar să se convertească la minute la ore; pentru această valoare de timp în minute pentru a fi împărțit la 60 și veți obține timp în ore: 30/60 = 0,5 ore.
• În acest exemplu, 120 kmh h = 0,5 x 60 km. Rețineți că unitatea de măsurători „oră“ este redusă și rămâne unitatea „km“ (adică distanța).

formula descrisă poate fi utilizată pentru calcularea valorilor sale membre. Pentru această valoare obosobte dorită pe o parte a formulei și să substituie o valoare în ea celelalte două variabile. De exemplu, pentru a calcula viteza cu ajutorul formulei s = d / t. și pentru a calcula timpul - t = d / s.

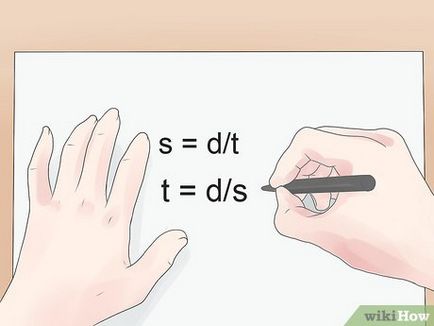
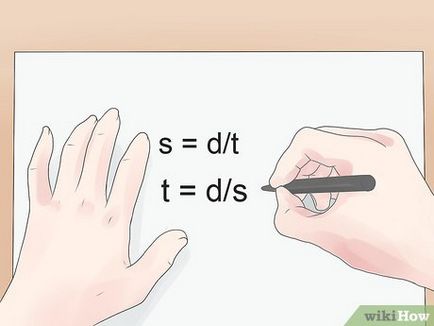
• Exemplu. Mașina a călătorit 60 km în 50 de minute. În acest caz, viteza este s = d / t = 60/50 = 1,2 km / min.
• Vă rugăm să rețineți că rezultatul este măsurată în km / min. Pentru a converti această unitate în km / h, rezultatul se înmulțește cu 60 pentru a obține 72 kmh.

Această formulă calculează viteza medie, adică se presupune că tot timpul cât în ​​modul în care corpul are o viteză constantă (invariabile). Este potrivit în cazul problemelor abstracte și modelarea mișcării corpurilor. În viața reală, se poate schimba viteza a corpului, care este, organismul poate accelera, încetini, opri sau se deplaseze în direcția opusă.

• In exemplul anterior, am constatat că mașina, conduce la 60 km în 50 de minute, călătorind cu o viteză de 72 de km / h. Acest lucru este valabil numai în condițiile în care viteza vehiculului nu sa schimbat în timp. De exemplu, în cazul în decurs de 25 minute (0,42 ore) vehiculul se deplasează cu o viteză de 80 km / h, iar pentru încă 25 de minute (0,42 ore) - la o viteză de 64 km / h prea va circula 60 km în 50 minute (80 x 0,42 + 64 x 0,42 = 60).
• Pentru a rezolva problemele, inclusiv variația vitezei corpului, este mai bine să utilizeze instrumentele derivate, mai degrabă decât formula de calcul a vitezei de la distanța și timpul.

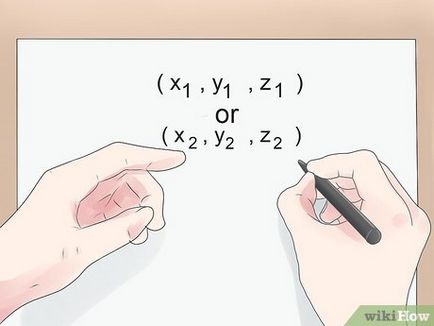
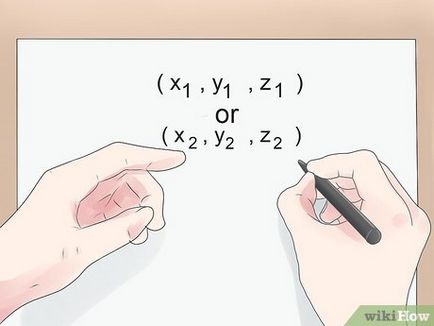
Găsiți două puncte ale coordonatelor spațiale. Dacă ați sunt date două puncte fixe, apoi, pentru a calcula distanța dintre aceste puncte, este necesar să se cunoască coordonatele lor; în spațiul unidimensional (pe linia reală) aveți nevoie de x1 și x2 coordonatele. în spațiul bidimensional - coordonatele (x1, y1) și (x2, y2), în spațiul tridimensional - coordonatele (x1, y1, z1) și (x2, y2, z2).

Se calculează distanța în spațiul unidimensional (punctele se află pe aceeași linie orizontală) cu formula: d = | x2 - x1 |. că este, scazi „x“ coordonatei, și apoi găsiți unitatea valorii.

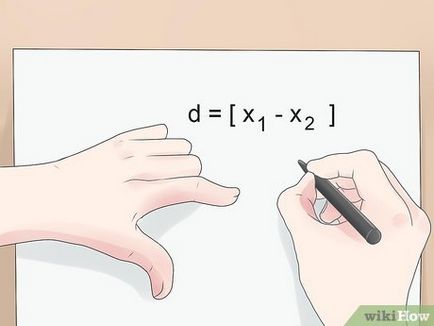
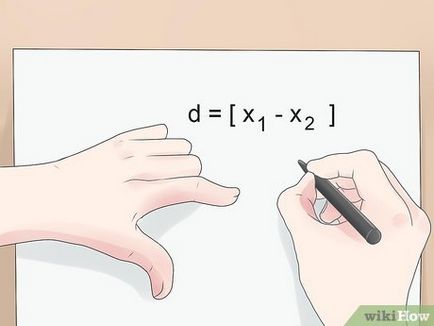
• De notat că în formula include modulul între paranteze (valoare absolută). Numărul de module - o valoare non-negativă a acestui număr (de exemplu, număr negativ este egal cu acest număr cu semnul plus).
• Exemplu. Mașina este situată între cele două orașe. Orasul, care se află în fața ei, la 5 km distanță, iar orașul în spatele ei - 1 km. Calculați distanța dintre orașe. Dacă luăm mașina pentru un punct de referință (la 0), coordonatele primului x1 oraș = 5, iar al doilea x2 = -1. Distanța dintre orașele:
  • d = | x2 - x1 |
  • = | -1-5 |
  • = | -6 | = 6 km.

Se calculează distanța în spațiul bidimensional conform formulei: d = √ ((x2 - x1) 2 + (y2 - y1) 2). Adică, scădeți poziția „x“, scade coordonatele „y“, erecte valorile obținute în piață, cutii de pliere, și apoi din valoarea rezultată a rădăcinii pătrate.

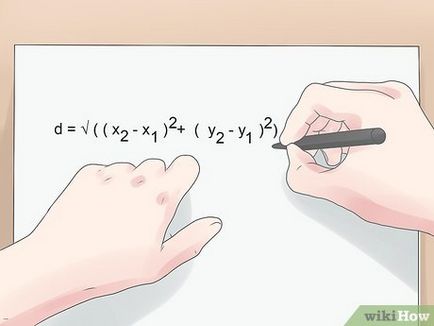
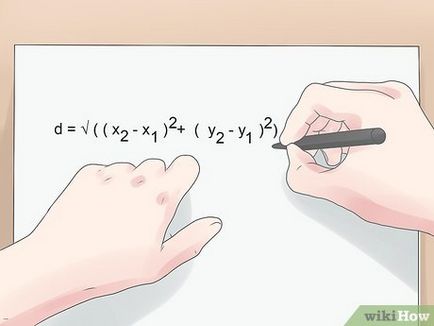
• Formula de calcul a distanței în spațiul bidimensional bazat pe teorema lui Pitagora, care prevede că ipotenuza unui triunghi dreptunghic este egală cu rădăcina pătrată a sumei pătratelor ambelor picioare.
• Exemplu. Găsiți distanța dintre două puncte cu coordonatele (3, -10) și (11, 7) (centrul cercului și un punct de pe cerc, respectiv).
• d = √ ((x2 - x1) 2 + (y2 - y1) 2)
• d = √ ((11-3) 2 + (7--10) 2)
• d = √ (64 + 289)
• d = √ (353) = 18,79

Se calculează distanța în spațiu tridimensional conform formulei: d = √ ((x2 - x1) 2 + (y2 - y1) 2 + (z2 - z1) 2). Această formulă este o formulă modificată pentru calcularea distanței în spațiu bidimensional cu adăugarea a treia coordonată «z».

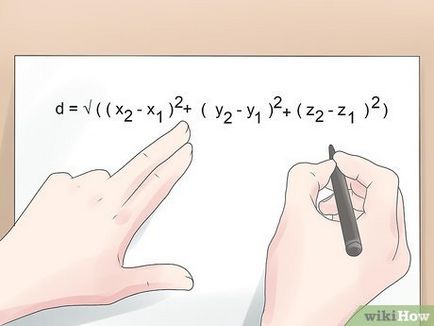
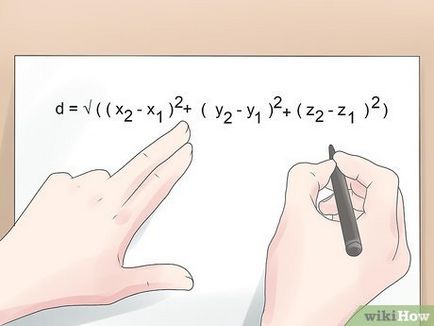
• Exemplu. Cosmonaut este într-un spațiu deschis, în apropierea celor doi asteroizi. Primul dintre acestea este un 8 km inainte de astronaut 2 km dreapta și la 5 km sub ea lui; al doilea asteroid se află la 3 km în spatele cosmonaut, la 3 km în partea stângă a acesteia, și la 4 km deasupra acesteia. Astfel, coordonatele asteroidului (8,2, -5) și (-3, -3,4). Distanța între asteroizi se calculează după cum urmează:
• d = √ ((- 3 - 8) 2 + (cu 3 - 2) 2 + (4 - 5) 2)
• d = √ ((- 11) 2 + (-5) 2 + (9) 2)
• d = √ (121 + 25 + 81)
• d = √ (227) = 15.07 km