Aria paralelogramului format de vectorii - formula, exemple de calcule
Aria paralelogramului formată de vectori este egală cu produsul dintre lungimile acestor vectori la un unghi colț care se află între ele.
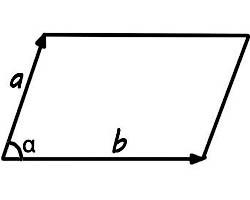
Ei bine, atunci când termenii sunt date lungimea acestor aceiași vectori. Cu toate acestea, se întâmplă, de asemenea, că pentru a aplica zona formulei paralelogramului construit pe vectorii este posibilă numai după decontarea coordonatelor.
Dacă ești norocos, iar termenii sunt vectori de lungime, trebuie doar să aplice o formulă pe care le-am analizat în detaliu zona paralelogramului în articol. Dimensiunea va fi egală cu produsul dintre sinusul module unghi între acestea:
Luați în considerare exemplul de calcul al zonei paralelogramului construit pe vectorii.
Obiectiv: paralelogram construit pe vectorii și. Zona de căutare, în cazul în care unghiul dintre ele de 30 °.
Exprima vector prin valorile lor:
Poate că aveți o întrebare - în cazul în care a făcut zerouri? Este demn de amintit că lucrăm cu vectori, și pentru ei. De asemenea, rețineți că în cazul în care, ca rezultat obținem expresia, acesta va fi convertit în. Acum vom efectua calculul final:
Să ne întoarcem la problema atunci când vectorii de lungime nu sunt specificate în condițiile. Dacă paralelogram dvs. se află în sistemul de coordonate carteziene, va trebui să faceți următoarele.
Calcularea lungimilor laturilor cifrele date de coordonatele
Pentru a găsi coordonatele vectorilor de început și sfârșit coordonatele scade din coordonatele corespunzătoare care încep. Să presupunem coordonatele vectorului a (x1, y1, z1) și vectorul b (x3, y3, z3).
Acum vom găsi lungimea fiecărui vector. În acest scop, fiecare coordonată urmează să fie pătrat, iar apoi stabilesc rezultatele și a unui număr finit de extract de rădăcină. Conform calculelor noastre vectori sunt următoarele:
Acum, trebuie să găsiți produsul nostru interior al vectorilor. În acest scop, se adaugă și multiplicate coordonatele lor respective.
Cu lungimea vectorilor și produsul lor scalar, putem găsi cosinusul unghiului situată între ele.
Acum putem găsi sinusul același unghi:
Acum avem toate valorile necesare, și putem găsi cu ușurință aria paralelogramului construit pe vectorii cu formula deja cunoscută.
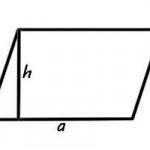
- Suprafața unui paralelogram
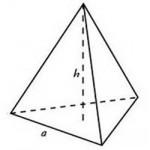
- Volumul piramidei triunghiulare
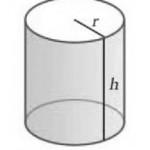
- Suprafața cilindrului
- Formula Huygens pentru calcularea lungimii arcului
- Zona de piramidă triunghiulară
